An overview of the paper “Do Deeper Convolutional Networks Perform Better?”. The authors review and analyze the effect of increasing depth on test performance. All images and tables in this post are from their paper.

Introduction

Traditional statistical learning theory argues that over-parameterized models will overfit training data and thus generalize poorly to unseen data. However, it is observed that although, over parametrized neural networks are capable of perfectly fitting training data, these networks often perform well on the test data, thereby contradicting classical learning theory. Recent work on double descent curve explains this phenomenon, showing that increasing the model capacity past the interpolation threshold can lead to a decrease in test error. Here, the authors hold the depth constant, and increase the width of the neural network. In this paper, the authors work on increasing the model capacity by increasing the depth of the model. Therby, adding an additional corollary that beyond a critical depth, the test performance worsens. This would suggest that double descent does not happen via depth.

Experimental Results

Bias vs Variance in CNN

After studying the bias-variance decomposition of deep CNNs, the authors showed that as depth increases, the bias decreases and variance increases, and thus, overall risk decreases. However, this is not on the interpolation regime. In the interpolation regime, it is true that deeper networks have increased risk. Furthermore, other authors also studied the optimization in deep CNNs and showed that increasing depth increases representational power, while increasing width smooths the optimization landscape. However, these works identified forms of implicit regularization, they do not provide an explicit connection to generalization in CNNs used for classification.

Empirical Evidence in Non-linear Classifiers

With fully-convolutional Networks

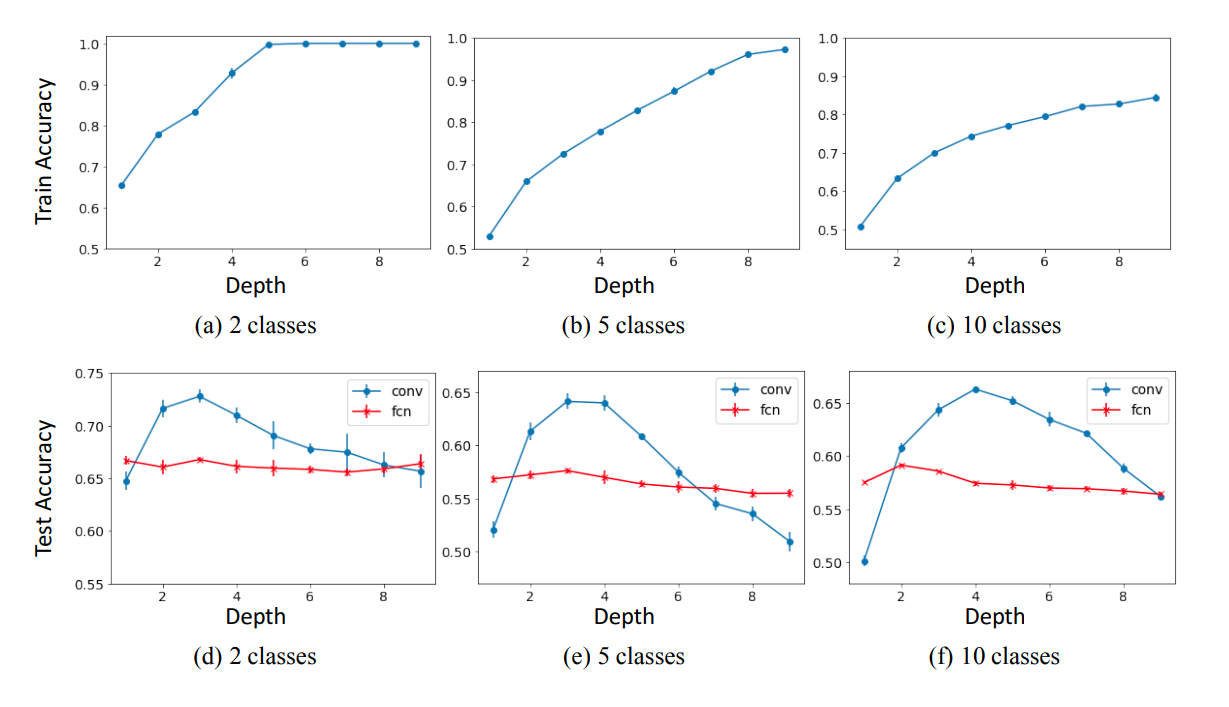
Here, the model is purely made of convolutional layers, batchnorm and non linear activation. It does not depend on other components commonly found in deep learning architectures such as residual connections, dropout, etc. The results from this experiment are as follows:

• As depth increases. training accuracy becomes 100%. However, beyond a critical depth threshold, the test accuracy begins to degrade sharply.
• Moreover, the value of the critical depth appears to increase as the number of training classes increases.
• As depth increases, test performance appears to approach that of a fully connected network.

Train and test accuracy of the Fully-Conv Net as a function of depth, for CIFAR10 input images.

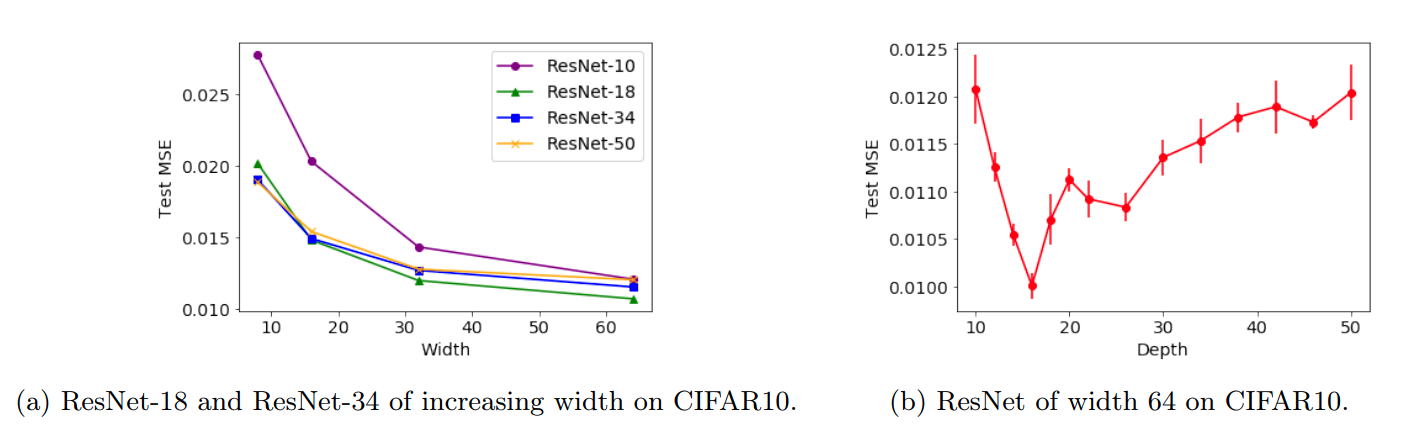
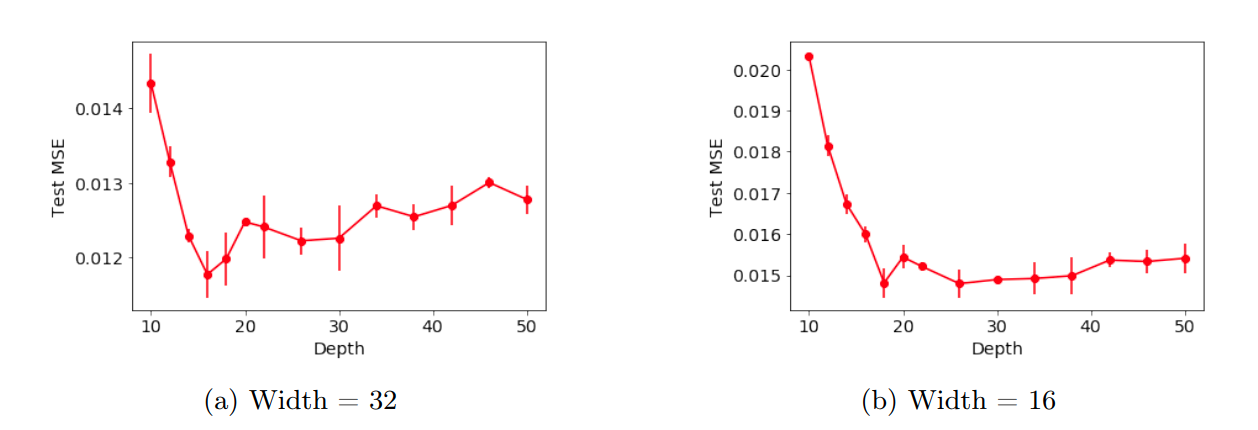
With Modern Deep learning Methods

Similar to previous experiment, increasing depth beyond a critical point, leads to an increase in test error. Furthermore, increasing depth in later blocks of Resnet leads to a more drastic increase in test error than compared to increasing depth in earlier blocks.

Train and Test losses of the ResNet models for all widths.

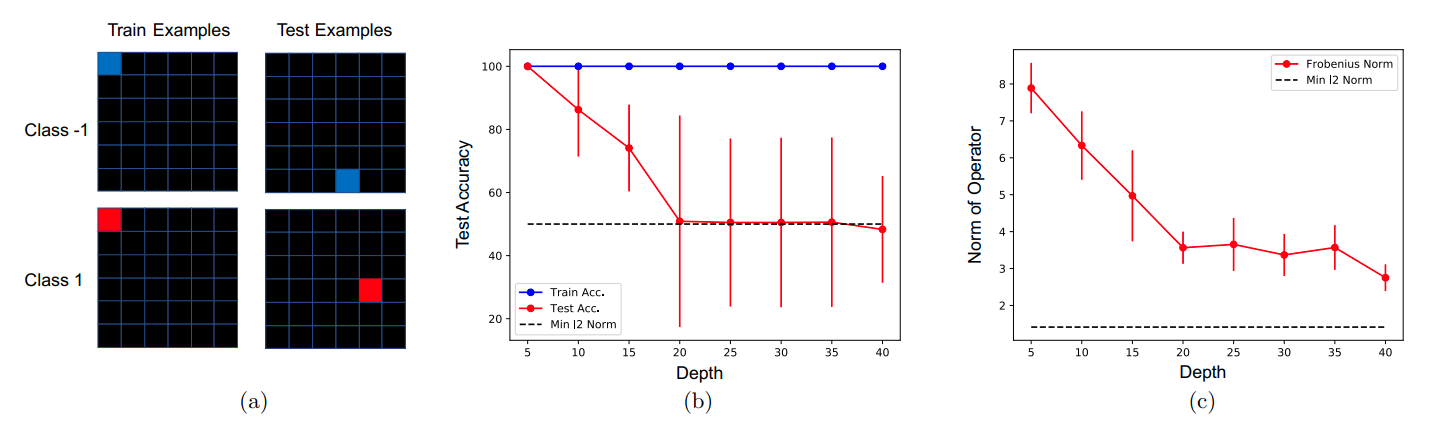
The Role of Depth in Linear Neural Networks

Here, the authors provide an example where fully connected networks do not generalize, and in which linear convolutional classifiers of increasing depth converge to this non-generalizing solution. The same also applies to linear autoencoders.

A toy example demonstrating that increasing depth in linear convolutional networks leads to operators of decreasing L2 norm, which manifests as a decrease in test accuracy.