An overview of the paper “Entropy SGD-Biasing Gradient Descent into Wide Valleys”. This paper proposes a new optimization algorithm called Entropy-SGD for training deep neural networks that is motivated by the local geometry of the energy landscape. The authors leverage upon this observation to construct a local-entropy-based objective function that favors well-generalizable solutions lying in large flat regions of the energy landscape, while avoiding poorly-generalizable solutions located in the sharp valleys. All images and tables in this post are from their paper.

Introduction

Local minima that generalize well and are discovered by gradient descent lie in “wide valleys” of the energy landscape, rather than in sharp, isolated minima. Almost-flat regions of the energy landscape are robust to data perturbations, noise in the activations, as well as perturbations of the parameters, all of which are widely-used techniques to achieve good generalization. Before we get into the exact proposed methodology, it would be useful to understand “Stochastic Gradient Langevin dynamics” and “Gibbs distribution” concretely.

Stochastic Gradient Langevin dynamics

The stochastic gradient Langevin dynamics (SGLD) has close connections to the Brownian motion. Suppose we have a brownian motion sampled such that . The idea in SGLD has close connections to Physics. Suppose there is a force on an object downwards. Unlike the ideal scenario where the particle goes exactly downwards (similar to SGD), there would be diffusion due to particles colliding with each other. Under this case, the particle will follow a brownian motion downwards, something SGLD tries to capture. Instead of going straight downwards, it adds a random noisy term which depicts the diffusion process. Under this scneario, the weight upgrade would go as follows:

Intuitively, this works similar to using gradient descent, but adding a noise when doing so. This would provide a chance for the model to escape local optima using this noise. This approach is predominantly used with annealing of noise such that the model would be able to reach global optima when trained for enough timesteps.

Gibbs distribution

The Gibbs distribution is also connected to statistical mechanics, where we denote the probability of observing a particle is directly proportional to the exponential of the negative energy of the system:

where is a constant, and is the energy of the system. In this work, they update the Gibbs distribution by adding a regularizer term that ensures the neighborhood is close to .

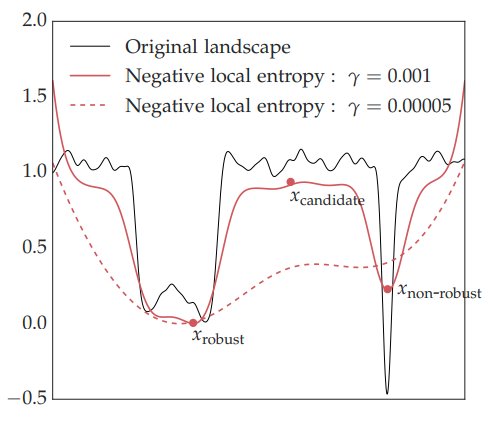
Local Entropy

Instead of minimizing the original loss , the authors propose to maximize:

The above is a log-partition function that measures both the depth of the valley at a location and it’s flatness through the entropy; called ‘local entropy’. The parameter biases the modified loss function towards . In this work, they set the inverse temperature to 1 because affords a similar control on the Gibbs distribution as well.

Furthermore, an interesting point highlighted in the paper is that critical points with high training error are exponentially likely to be saddle points with many negative directions and all local minima are likely to have error that is very close to that of the global minimum.

Local entropy concentrates on wide valleys in the energy landscape.