An overview of the paper “La-MAML: Look-ahead Meta-Learning for Continual Learning”. The authors propose an algorithm for look-ahead meta-learning that is model-agnostic. All images and tables in this post are from their paper.

The continual learning (CL) problem involves training models with limited capacity to perform well on a set of an unknown number of sequentially arriving tasks. The continual learning problem is commonly studied in the literature by partitioning a static dataset into a disjoint subset of tasks, for example, partitioning a 100 class dataset into 20 sets of 5-way classification tasks. The data from these tasks is then seen by the model as sequential streams and the model is evaluated at the end of each task’s stream on the set of all tasks seen thus far. Catastrophic forgetting is one of the biggest challenges in this setup. Catastrophic forgetting is the tendency of an artificial neural network to completely and abruptly forget previously learned information upon learning new information. This occurs because the i.i.d. sampling condition required by stochastic gradient descent are violated when the data from different tasks arrive sequentially.

Catastrophic Forgetting

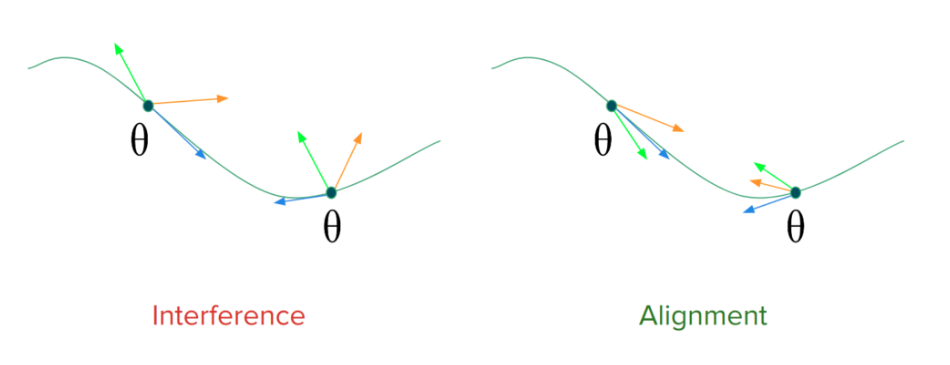
One way to look at the problem of forgetting is through gradient interfence and gradient alignment. Let’s consider 2 tasks. Suppose, the task-wise gradients for a model’s parameters conflict with each other in certain parts of the parameter space. The performance would thus degrade on the old tasks because the gradient updates made while learning a new task don’t align with gradients directions for old tasks. On the right of the image is an ideal scenario, where the gradients align and therefore progress on learning a new task, which coincides with progress on the old ones. Ensuring gradient-alignment is therefore essential to make shared progress on task-wise objectives under limited availability of training-data. This kind of alignment across tasks can be achieved by exploiting some properties of meta-learning based gradient updates.

Gradient direction for various tasks at time t.

Model Agnostic Meta-Learning (MAML)

Suppose, we want to train a model to be good at learning from a handful of samples from any data distribution, such that it performs well on unseen samples of distribution. We can think of this as wanting to optimize two objectives, the one we minimize when we learn on the handful of samples (or L_inner) and the one we test the model once it has completed learning on the handful of samples (let’s call this L_outer, evaluated on unseen samples from the distribution). This intuitively makes sense, because the only way to make progress on unseen data (seen for Louter) is to somehow have the gradients on that data be aligned with the actual gradient steps taken by the model on some seen data (seen during Linner) (in this case, the few-shot samples).

Gradient Alignment

Gradient Episodic Memory solves a quadratic program to get the gradient direction that maximally aligns with the gradient on old and new tasks, A-GEM simply clips the gradients on new tasks such that they have no component that interferes with old tasks. Meta-Experience Replay (MER) realized that the gradient-alignment based objective of GEM was roughly equivalent to that of first order meta learning algorithm Reptile and proposed a replay-based meta-learning algorithm that learned a sequence of tasks while increasing alignment between task-wise objectives.

Online-Aware Meta Learning (OML)

This approach proposed pre-training a representation through meta-learning, using catastrophic forgetting as the learning signal in the outer objective. The parameters of a representation learning network (RLN) are fixed, and a task learning algorithm (TLN) further processes the representation and learns continually from a stream of incoming samples. After short intervals, the RLN+TLN is repeatedly evaluated on a set of held-out tasks to measure the forgetting that would’ve taken place. The meta-learning signal, when ackpropogated to the RLN over many epochs leads to it learning a representation that is resistant to the catastrophic forgetting. This composition of two losses to simulate continual learning in the inner loop and test forgetting in the outer loop is referred to as the OML objective.

How La-MAML works

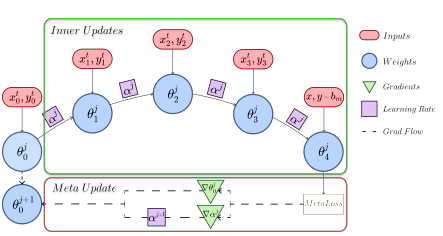
It seems like a natural solution is to optimise the OML objective online for all the parameters of a model through a MAML update. Here, the inner objective would be to learn from the incoming data in the streaming task while the outer objective would be to test the adapted parameters on data sampled from all the tasks seen so far. Since data is available only while it is streaming, we could sub-sample and store some of it in a replay buffer and later sample data from it for evaluation in the outer objective. The authors derive the gradients of the MAML objective and show their equivalence to that of AGEM’s objective in the paper. The authors also show that their version of the meta-objective learns faster – since it aligns the average gradient on the old task data with the gradient on the new task’s data instead of trying to align all tasks’ gradients with each other (as in MER). The gradient alignment even across the old tasks still remains positive throughout training even when not explicitly incentivized. For every batch of data, the initial weights undergo a series of fast updates to obtain (here ), which is evaluated against a meta-loss to backpropagate gradients with respect to the weights and LRs . First is updated to which is then used to update to . This is motivated by thier observation that the expression for the gradient of the OML objective with respect to these LRs directly reflects the alignment between the old and new tasks. Here, gradient of alpha is equal to the dot product of [change in ] and [negative of change in ]. C-MAML uses a fixed learning rate.

La-MAML Algorithm.