An overview of the paper “Learning Individual Causal Effects from Networked Observational Data”. The author proposes a novel approach to infer confounders froom social networks, which allows us to learn valid causal effects from observational data. All images and tables in this post are from their paper.

Introduction

In short, confounders are variables that causally influence both the treatment and the outcome. For example, the poor socioeconomic status of an individual can limit her access to an expensive medicine and have negative impact on her health condition at the same time. Thus, without controlling the influence of the socioeconomic status, we may overestimate the treatment effect of the expensive medicine. To exploit network patterns for mitigating confounding bias, the authors propose the network deconfounder, a novel causal inference framework that captures the influence of hidden confounders from both the original feature space and the auxillary network information. An introduction of the background knowledge of learning individual causal effects are given below:

• Potential Outcomes: Given an instance and the treatment , the potential outcome is denoted by .
• Individual Treatment Effect (ITE): The ITE is defined as the expected potential outcome of an instance under treatment subtracted by that under control, which reflects how much improvement in the outcome would be based by the treatment.

• Average Treatment Effect (ATE): With ITE defined, the ATE is computed by taking the average of ITE.
• Strong Ignorability: With strong ignorability, it is assumed that: ** Potential outcomes of an instance are independent of whether it receives treatment or control given its features. ** For each instance, the probability to get treated lies between 0 and 1. ** This would imply that .

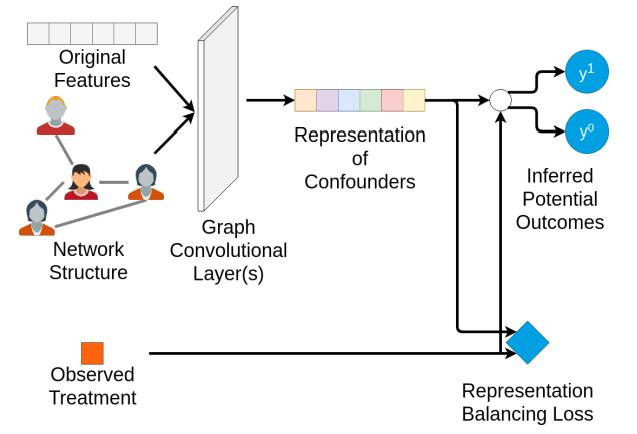
Workflow of proposed framework.

Network Deconfounder

In this work, the authors do not assume strong ignorability, and that the dependencies between the treatment variables and two potential outcomes are introduced by hidden cofounders. Instead, they make a more practical and weaker assumption, that the features and the network structure are two sets of proxy variables of the hidden confounders. For example, although we cannot directly measure the socioeconomic status of an individual, we can collect features such as age, job type, zip code, and the social network to approximate her socioeconomic status. Based on this assumption, the proposed network deconfounder attempts to learn representations that approximate hidden confounders and estimate ITE from networked observational data simultaneously. However, leveraging the underlying network structure for controlling confounding bias raises two challenges, the failure of i.i.d. when it comes to the feature distribution, and a very sparse network. To tackle these challenges of controlling confounding bias when network structure information exists, the authors propose to divide the task into two steps:

• First, we aim to learn representations of hidden confounders by mapping the features and the network structure simultaneously into a shared representation space of confounders.
• An output function is learned to infer a potential outcome of an instance based on the treatment and the representation of hidden confounders.

Learning Representation of Confounders

The first component of the network deconfounder is a representation learning function . The function maps the features and the underlying network into the -dimensional() shared latent space of confounders. The function is parametrized using Graph Convolutional Networks.

Inferring Potential Outcomes

The second component maps is the function such that . This maps the representation of hidden cofounders as well as a treatment to the corresponding outcome. The output of this component is as follows:

Objective function

The objective function of the network deconfounder can be broken into three parts:

• Factual Outcome Inference: First, we aim to minimize the error in the inferred factual outcomes. It is defined as:

• Representation Balancing: Minimizing the error in factual outcomes, does not necessarily mean that the error in counterfactual outcomes is also minimized. In particular, the network deconfounder would be trained on the conditional distribution of factual outcomes and the task is to infer the conditional distribution of counterfactual outcomes .
• L2 Regularization: We apply a squared L2 norm of the model weights to prevent the weights from blowing up and overfitting.

Conclusions

In this paper, the authors study a novel problem, learning individual treatment effects from networked observational data. As the underlying network structure could capture useful information of hidden confounders, we propose the network deconfounder framework, which leverages network structural patterns along with original features for learning better representations of confounders. This paper has opened two new research problems:

• Using temporal dependencies to capture patterns of hidden Confounders
• Expoloiting dynamic graphs for the same.

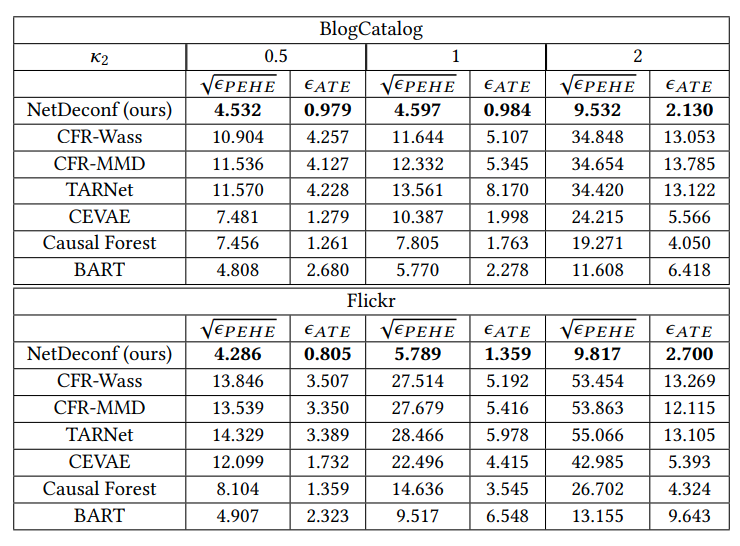
Experimental Results comparing effectiveness of the proposed network deconfounder with the baseline methods.