An overview of the paper “Learning an Embedding Space for Transferable Robot Skills”. The author presents a method for reinforcement learning of closely related skills that are parameterized via a skill embedding space. All images and tables in this post are from their paper.

Introduction

The idea is to learn such skills by taking advantage of latent variables and exploiting a connection between reinforcement learning and variational inference. The main contribution of their work is an entropy regularized policy gradient formulation for hierarchical policies, and an associated, data-efficient and robust off-policy gradient algorithm based on stochastic value gradients. They also show that, the proposed technique can interpolate and/or sequence previously learned skills in order to accomplish more complex tasks, even in the presence of sparse rewards. Their method learns manipulation skills that are continuously parameterized in an embedding space. The authors show how to take advantage of these skills for rapidly solving new tasks, effectively by solving the control problem in the embedding space rather than the action space.

Preliminaries

The authors perform reinforcement learning in Markov Decision processes (MDP). We denote state the continuous state of the agent; denotes the action in . Actions are drawn from a policy distribution , with parameters ; in this case, a Gaussian distribution whose mean and diagonal covariance are parameterized via a neural network. At every step the agent receives a scalar reward and we consider the problem of maximizing the sum of discounted rewards .

Learning Versatile Skills

The general goal of the method is to re-use skills learned for an initial set of tasks to speed up - or in some cases even enable - learning difficult target tasks in a transfer learning setting.

The authors train a multi-task setup, where the task id is given as one-hot input to the embedding network. The embedding network generates an embeedding distribution that is sampled and concatenated the current observation to serve as input to the policy. After interacting with the environment, a segment of states is collected and fed into the inference network. The inference network is trained to classify what embedding vector the segment of states was generated from.

Summary of proposed approach.

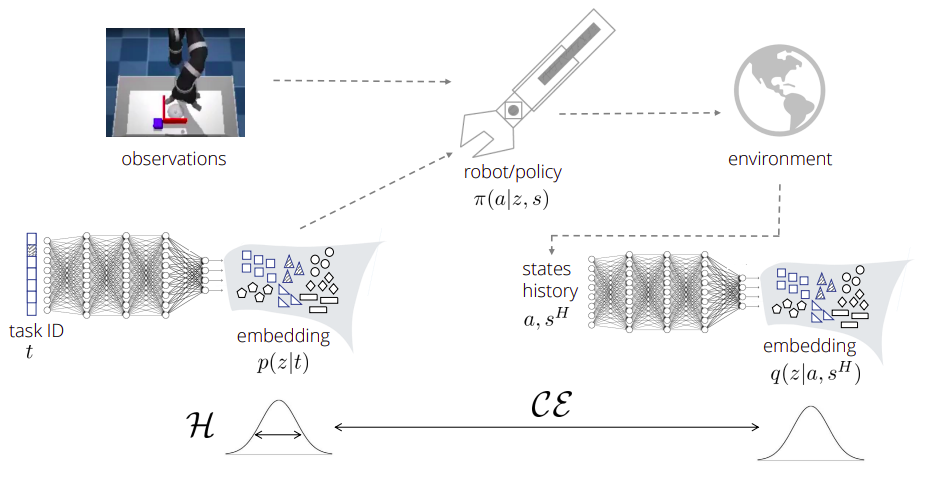
Policy Learning via a Variational Bound on Entropy Regularized RL

To learn the skill-embedding, we assume to have access to a set of initial tasks with accompanying, per-task reward functions , which could be comprised of different environments, variable robot dynamics, reward functions, etc. During training time, we provide access to the task id (indicaating which task the agent is operating in) to our RL agent. To obtain data from from all training tasks for learning - we draw a task and its id randomly from the set of tasks at the beginning of each episode and execute the agents current policy it it.

For our policy to learn a diverse set of skills instead of just seperate solutions (one per task), we endow it with a task-conditional latent variable . The idea is that, with latent variable could also be called “skill embeddings”, where the policy is able to represent a distribution over skilss for each task and to share these across tasks. In the simplest case, this latent variable could be resampled at every timestep and the state-task conditional policy would be defined as . One option would be to let , in which case the policy would correspond to a mixture of subpolicies.

Introducing a latent variable facilitates the representation of several alternative solutions but it does not mean that several alternative solutions will be learned. To achieve this, the authors formulate the objective as an entropy regularized RL problem:

where is the initial state distribution, is the weighting term - trading the arbitrarily scaled reward against the entropy - and we can define to denote the expected return for task (under policy ) when starting from state and taking action . The entropy regularization term is defined as: . With some mathematical rigor, the authors adapt the above regularization term to work in the setting of latent variables.

The resulting equation maximizes the entropy of the embedding given the task and the entropy of the policy conditioned on the embedding (thus, aiming to cover the embedding space with different skill clusters). The negative CE encourages different embedding vectors to have different effects in terms of executed actions and visited states: Intuitively, it will be high when we can predict from resulting action , .

Learning an Embedding for Versatile Skills in an Off-Policy Setting

The objective presented above could be optimized directily only in an on-policy setting. To optimize in the off-policy setting, some minor approximations are required. The authors assume that the availability of a replay buffer (containing full trajectory execution traces including states, actions, task id and reward), that is incrementally filled during training. Additional to the trajectory traces, we also store the probabilities of each selected action and denote them with the behavior policy probability as well as the behaviour probabilities of the embedding . Given this replay data, we formulate the off-policy perspective of our algorithm as follows:

• We start with the notion of a lower-bound Q-function that depends on both state and action and is conditioned on both, the embedding and the task id .
• This encapsulates all time dependent terms from previous equation:

The exact math to train the embedding network, and inference network is best described in the paper.

Learning to Control the Previously-Learned Embedding

Once the skill-embedding is learned using the described multi-task setup, we utilize it to learn a new skill. There are multiple possibilities to employ the skill-embedding in such a scenario including fine-tuning the entire policy or learning only a new mapping to the embedding space.In this work, the authors focus on the latter: To adapt to a new task we freeze the policy network and only learn a new state embedding mapping via a neural network (parameterized by parameters ). On other words, we only allow the network to learn how to modulate and interpolate between the already-learned skills, but we do not allow to change the underlying policies. The authors support the efficiacy of their model by training on multiple tasks.