An overview of the paper “Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks”. The authors propose an algorithm for meta-learning that is model-agnostic. All images and tables in this post are from their paper.

The goal of meta-learning is to train a model on a variety of learning tasks, such that it can solve new learning tasks using only a small number of training samples. Here, the parameters of the model are explicitly trained such that a small number of gradient steps with a small amount of training data from a new task will produce good generalization performance on that task. In effect, the method trains the model to be easy to fine-tune.

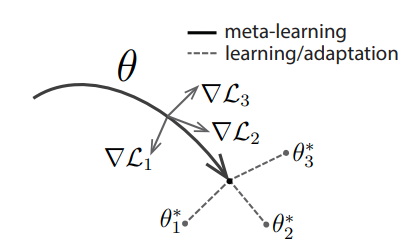
Model-agnostic meta-learning algorithm.

Catastrophic Forgetting

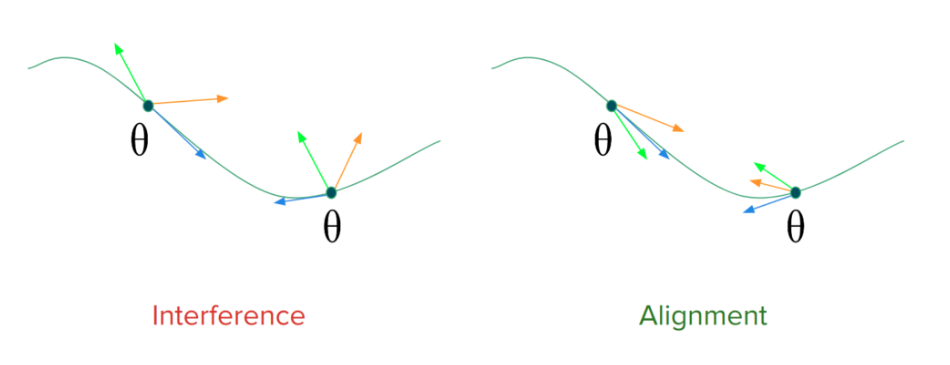
One way to look at the problem of forgetting is through gradient interfence and gradient alignment. Let’s consider 2 tasks. Suppose, the task-wise gradients for a model’s parameters conflict with each other in certain parts of the parameter space. The performance would thus degrade on the old tasks because the gradient updates made while learning a new task don’t align with gradients directions for old tasks. On the right of the image is an ideal scenario, where the gradients align and therefore progress on learning a new task, which coincides with progress on the old ones. Ensuring gradient-alignment is therefore essential to make shared progress on task-wise objectives under limited availability of training-data. This kind of alignment across tasks can be achieved by exploiting some properties of meta-learning based gradient updates.

Gradient direction for various tasks at time t.

Model Agnostic Meta-Learning (MAML)

Suppose, we want to train a model to be good at learning from a handful of samples from any data distribution, such that it performs well on unseen samples of distribution. We can think of this as wanting to optimize two objectives, the one we minimize when we learn on the handful of samples (or ) and the one we test the model once it has completed learning on the handful of samples (let’s call this , evaluated on unseen samples from the distribution). This intuitively makes sense, because the only way to make progress on unseen data (seen for ) is to somehow have the gradients on that data be aligned with the actual gradient steps taken by the model on some seen data (seen during ) (in this case, the few-shot samples). In the K-shot learning setting, the model is trained to learn a new task drawn from from only samples drawn from and feedback . The model is then improved by considering how the test error on new data from changes with respect to parameters. In effect, the test error on sampled tasks serves as the training error of the meta-learning process. At the end of meta-training, new tasks sampled from , and meta performance is measured after learning from samples.

The aim is to find model parameters that are sensitive to changes in the task, such that small changes in the parameters will produce large improvements on the loss function of any task drawn. The complete algorithm can be broken down into few simple steps:

• Create disjoint subset of tasks (eg. dogs, cats, etc.)
• Make inner updates using one task and repeat for all tasks
• Do an overall updation using all the losses, thus obtained, outer update.

MAML Algorithm.