Neural Network Attributions- A causal Perspective

An overview of the paper “Neural Network Attributions- A causal Perspective”. The author proposes a new attribution method for neural networks developed using first principles of causality. All images and tables in this post are from their paper. The neural network architecture is viewed as a Structural Causal Model, a nd a methodology to compute the causal effect of each feature on the output is presented. Formally, attributions are defined as the effect of an input feature on the prediction function’s output. This is an inherently causal question. While gradients answer the question “How much would perturbing a particular input affect the output?”, they do not capture the causal influence of an input on a particular neuron. The author’s approach views the neural network as a structural causal model (SCM) and proposes a new method to compute the Average Causal Effect of an input on an output neuron.

Attributions of Neural Network Models

Attribution is defined as “effect of an input feature on the prediction function’s output”. This is inherently a causal question. Previous methods such as Gradient-based methods ask the question “how much would perturbing a particular input affect the output?”. This is not a causal analysis. Other methods also include surrogate models (or interpretable regressors) which is usually correlation based. Surrogate model is a different model that hopes to explain the weights learned by the neural network.

Gradient-based and Perturbation-based methods could be viewed as special cases of Individual Causal Effect.

$ICE^y_{do(x_i=\alpha)} = y_{x_i=\alpha}(u) - y(u)$

We intervene and set $\alpha$ to $u_i + \epsilon$ . Note that gradient based approaches required to pass one specific example which was used to compute gradients. Such methods are sensitive and cannot give global attributions.

Neural Networks as Structural Causal Models (SCM)

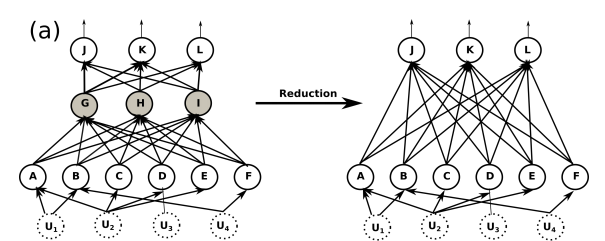
The authors begin by stating that neural network architectures can be trivially interpreted as SCMs. Note that the authors do not explicitly attempt to find the causal direction in this case, but only identify the causal relationships given a learned function. Neural networks can be interpreted as directed acyclic graphs with directed edges from a lower layer to layer above. The final output is thus based on a hierarchy of interactions between lower level nodes. Furthermore, the method works on the assumption that “Input dimensions are causally independent of each other” (they can be jointly caused by a latent confounder). Another assumption of the SCM is that the intervened input neuron is d-seperated from other input neurons. This would mean that, given an intervention on a particular variable, the probability distribution of all other input neurons does not change, i.e. for $x_j \neq x_i, P(x_j|do(x_i=\alpha)) = P(x_j)$

An $n$ layer feedforward neural network $N(l_1, l_2, ..., l_n)$ where $l_i$ is the set of neurons in layer $i$ has a corresponding SCM $M([l_1,l_2,...,l_n],U,[f_1,f_2,...,f_n],P_U)$ , where $l_1$ is the input layer, and $l_n$ is the output layer. Corresponding to every layer $l_i$ , $f_i$ refers to the set of causal functions for neurons in layer $i$ . $U$ refers to a set of exogenous random variables which act as causal factors for input neurons. THe SCM above can be reduced to an SCM $M'([l_1,l_n],U,f',P_U)$ . marginalizing the hidden neurons out by recursive substitution is analogous to deleting the edges connecting these nodes and creating new directed edges from the parents of the deleted neurons to their respective child vertices in the correspoinding Bayesian network.

Feedforward neural network as SCM.

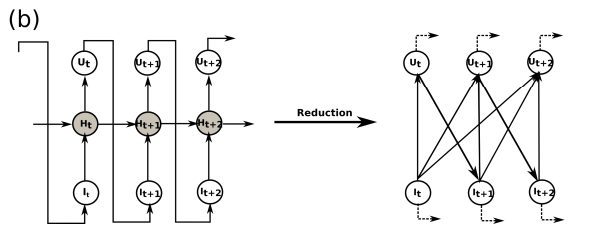
However in a RNN, defining an SCM is more complicated due to the feedback loops which makes the Bayesian network no longer acyclic. Due to the recurrent connections between hidden states, marginalizing over the hidden neurons (via recursive substitution) creates directed edges from input neurons at every timestep to output neurons at subsequent timesteps.

RNN as SCM.

Causal Attributions for Neural Network

This work attempts to address the question: “What is the causal effect of a particular input neuron on a particular output neuron of the network?”. This is also known as the “attribution problem”. We seek the information required to answer this question as encapsulated in the SCM $M'([l_1,l_n],U,f',P_U)$ consistent with the neural model architecture $N(l_1, l_2, ..., l_n)$ .

Average Causal Effect

The average causal affect (ACE) of a binary random variable $x$ on another random varialbe $y$ is commonly defined as $\mathbb{E}[y|x=1]-\mathbb{E}[y|x=0]$ . Given a neural network with input $l_1$ and output $l_n$ , we measure the ACE of an input feature $x_i$ on an output feature $y$ as:

$ACE_{x_i=\alpha}^{y} = \mathbb{E}[y|x_i=\alpha] - baseline_{x_i}$

Causal Attribution

We define $ACE_{x_i=\alpha}^{y}$ as the causal attribution of input neuron $x_i$ on an output neuron $y$ . An ideal baseline would be any point along the decision boundary of the neural network, where predictions are neutral. In this work, the authors propose the average ACE of $x_i$ on $y$ as the baseline value for $x_i$ , i.e. $baseline_{x_i} = \mathbb{E}_{x_i}[\mathbb{E}_{y}[y|x_i = \alpha]]$ .

Calculating Interventional Expectations

We refer to $\mathbb{E}[y|x_i = \alpha]$ as the interventional expectation of $y$ given the intervention $x_i = \alpha$ . Due to the curse of dimensionality, this unbiased estimate of interventional expectations would have a high variance. While every SCM $M'$ , obtained via marginalizing out the hidden neurons, registers a causal Bayesian network, this network is not necessarily causally sufficient. TO address this, the authors propose the following:

Given an $n$ layered feedforward neural network $N(l_1,l_2, ...,l_n)$ and its corresponding reduce SCM $M'$ , the intervened input neuron is d-seperated from all other input neurons.
Given an $n$ layered feedforward neural network $N(l_1,l_2, ...,l_n)$ and an intervention on neuron $x_i$ , the probability distribution of all other input neurons does not change.

Computing ACE using Causal Regressors

The ACE requires the computation of two quantities: the interventional expectation and the baseline. They defined the baseline value for each input neuron to $baseline_{x_i} = \mathbb{E}_{x_i}[\mathbb{E}_{y}[y|x_i = \alpha]]$ . The interventional expectation is a function of $x_i$ , as all other variables are marginalized out.

Overall Methodology

For feedforward networks, the calculation of interventional expectations is straightforward. The empirical means and covariances between input neurons can be precomputed from training data. Since calculating interventional expectations can be costly; so, we learn a causal regressor function that can approximate this expectation for subsequent on-the-fly computation of interventional expectations. The output of intervenentional expectations at different interventions of $x_i$ is used as training data for the polynomial class of functions.

Axioms of Attributions

In all below axioms, $F$ denotes the causal function. The axioms of attribution include:

Completeness - For any input $x$ , the sum of the feature attributions equals $F(x) = \sum_i A^F_i(x)$ .
Sensitivity - If $x$ has only one non-zero feature and $F(x)\neq 0$ , then the attribution to that feature should be non-zero.
Implementation Invariance - When two neural networks compute the same mathematical function $F(x)$ , regardless of how differently they are implemented, the attributions to all features should always be identical.
Linearity
Symmetry Preserving - For any input $x$ where the values of two symmetric features are the same, their attributions should be identical as well.

Gradient based methods violate sensitivity axiom. Some surrogate methods violate Implementation Invariance axiom.

Written on April 2, 2021