An overview of the paper “Unsupervised Learning via Meta-Learning”. In this paper, the authors propose a method to construct tasks from unlabeled data in an automatic way and run meta-learning over the constructed tasks. All images and tables in this post are from their paper. The authors note that when integrated with meta-learning, relatively simple task construction mechanisms, such as clustering embeddings, lead to good performance on a variety of downstream, human-specified tasks. Unlike unsupervised learning methods, meta-learning methods require large, labeled datasets and hand-specified task distributions. These dependencies are major obstacles to widespread use of these methods for few-shot classification. To overcome this, the authors propose a model such that- with only raw, unlabeled observations, the model’s goal is to learn a useful prior such that, after meta-training, when presented with a modestly-sized dataset for a human-specified task, the model can transfer its prior experience to efficiently learn to perform the new task. If we can build such an algorithm, we can enable few-shot learning of new tasks without needing any labeled data nor any pre-defined tasks. The core idea in this paper is that we can leverage unsupervised embeddings to propose tasks for a meta-learning algorithm, leading to an unsupervised meta-learning algorithm that is particularly effective as pre-training for human-specified downstream tasks.

Brief Overview of Methodology

Problem Statement

Our goal is to leverage unlabeled data for the efficient learning of a range of human-specified down- stream tasks. We only assume access to an unlabeled dataset during meta-training. After learning from the unlabeled data, which we will refer to as unsupervised meta-training, we want to apply what was learned towards learning a variety of downstream, human-specified tasks from a modest amount of labeled data, potentially as few as a single example per class. These downstream tasks may, in general, have different underlying classes or attributes (in contrast to typical semi-supervised problem assumptions), but are assumed to have inputs from the same distribution as the one from which datapoints in are drawn. In this setting, the upper bound (upper bound of the number of tasks) is assumed to be known during unsupervised meta-training. Otherwise, the values and (number of tasks, and number of samples per task) are not known apriori.

If such tasks are adequately diverse and structured, then meta-learning these tasks should enable fast learning of new, human-provided tasks.

• Random Partition: While such a scheme introduces diverse tasks, there is no structure; that is, there is no consistency between a task’s training data and query data, and hence nothing to be learned during each task, let alone across tasks.
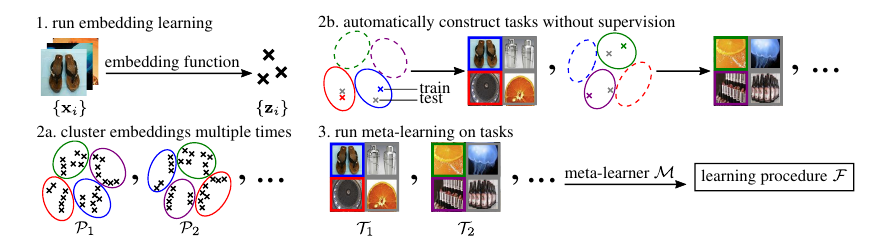
• k-means clustering: To construct tasks with structure that resembles that of human-specified labels, we need to group datapoints into consistent and distinct subsets based on salient features. However, the result of k-means is critically dependent on the metric space on which its objective is defined. Clustering in pixel-space is unappealing for two reasons: (1) distance in pixel-space correlates poorly with semantic meaning, and (2) the high dimensionality of raw images renders clustering difficult in practice.
• CACTUs: This is the proposed approach of the authors. Here, they use state-of-the-art unsupervised learning methods to produce useful embedding spaces. The KNN is run on top of this embedding space. To avoid imbalanced clusters dominating the meta-training tasks, we opt not to sample from , but instead sample clusters uniformly without replacement for each task. Here, each k-means resembles 1 task, and each cluster resembles labels.

Discussion

The authors demonstrate that meta-learning on tasks produced using simple mechanisms based on embeddings improves upon the utility of these representations in learning downstream, human-specified tasks. We can expect our method to yield better performance as the methods that produce these embedding functions improve, becoming better suited for generating diverse yet distinctive clusterings of the data. In principle, CACTUs-based meta-learning may outperform supervised meta-learning when the latter is trained on a misaligned task distribution. We leave this investigation to future work. While we have demonstrated that k-means is a broadly useful mechanism for constructing tasks from embeddings, it is unlikely that combinations of k-means clusters in learned embedding spaces are universal approximations of arbitrary class definitions.